The most basic form of showing "translation through rotation" is just to line up a bunch of circles (where "a bunch of" could mean "an infinite number of") but only show one point on each circle. There are lots of ways to pick this one point; a basic one is where a circle B, one unit to the right of circle A, shows a point 10\(^\circ\) farther around the circle that circle A. (This idea was given to us by NichG in a comment on the previously mentioned post, who also generated this image.)
Here is our take on this concept:
It may be hard to believe that each point is just moving in a circle, so we provide this image as "proof":
Each of the circles shown above has a center that lies on a horizontal line. We can put these circle centers on other curves to get different results. Below, we put the centers on a sine wave.
This is the basic structure of the image at the top of this post; we just varied the color a little according to its height to give the impression of a white-capped ocean wave.
Other Shapes
What if each point does not follow a circle, but some other path? Below, each point follows a square of unit length.
Again, since it can be hard to believe, we offer this image as proof:
We can also vary the way that we traverse this square. The red dot above travels at a constant speed around the square, covering each side in 1 time unit. In the following image, we traverse the square again at a rate of 1 side length per time unit, but slow down at the corners and speed up in the middle.
Notice how the sharp corners are smoothed out. To show the difference of the "traversing of the square," consider the following, where the two dots follow the same path at two different rates.
They arrive at each corner at different times, but the red dot slows down at the corners and speeds up in the middle, while the white dot travels at a constant speed.
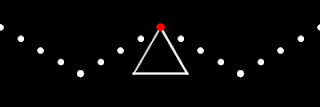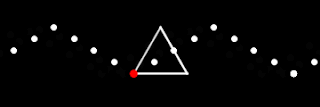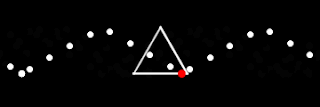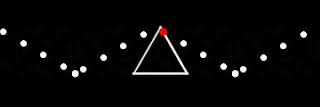
We also considered traveling along a triangle.
We have worked our way down from circles (which have "infinite sides"), to squares (with 4 sides) to triangles (3 sides, but you didn't need us to tell you that). To get even lazier with our motion, lets just move dots up and down.
The red dot is moving up/down at a constant speed; varying this so it goes up/down along a sine wave gives ...
... a sine wave.
We tried one more, moving a dot along a 5 pointed star.
We're not sure there is much point to this one, but we thought it was fun to try.
We would be interested in seeing any images like these that you think look cool. Post it somewhere and send us a link.
Consider following us on Twitter; we'll tweet only when a new post is up.
Our Code
We've gotten requests to show our code in the past. We haven't done it so far mostly out of shyness/embarrassment about the quality of our coding, but we'll show some of it here. We write in Mathematica.
All of the images are created using the same basic workflow. Use a Manipulate environment to test the image; the change the "Manipulate" to "Table" to create a set of frames, then Export these frames to a gif.
Here is the code to do the basic circles at the top. Change f[x_]:=0 to f[x_]:=Sin[x] to get the circles with centers along the sine wave.
f[x_] := 0
Manipulate[
Show[ListPlot[
Table[{Cos[i - a], Sin[i - a]} + {i, f[i]}, {i, -5, 5, .5}],
PlotRange -> {{-5, 5}, {-1.5, 1.5}},
PlotStyle -> {White, PointSize[.02]}, Axes -> None,
AspectRatio -> Automatic, Background -> Black],
ParametricPlot[{{Cos[t], Sin[t]}, {Cos[t - 3] - 3,
Sin[t - 3]}, {Cos[t + 3] + 3, Sin[t + 3]}}, {t, 0, 2 Pi},
PlotStyle -> {{White}}],
ParametricPlot[{{Cos[t], Sin[t]}, {Cos[t - 3] - 3,
Sin[t - 3]}, {Cos[t + 3] + 3, Sin[t + 3]}}, {t, 0, 2 Pi},
PlotStyle -> {{Thickness[.005], White, Opacity[.6]}}],
ListPlot[{{Cos[-a], Sin[-a]}, {Cos[-3 - a] - 3,
Sin[-a - 3]}, {Cos[-a + 3] + 3, Sin[-a + 3]}},
PlotStyle -> {{PointSize[.025], Red}}], Axes -> None], {a, 0, 2 Pi,2 Pi/30}]
basicRotationframes =
Table[Show[
ListPlot[
Table[{Cos[i - a], Sin[i - a]} + {i, f[i]}, {i, -5, 5, .5}],
PlotRange -> {{-5, 5}, {-1.5, 1.5}},
PlotStyle -> {White, PointSize[.02]}, Axes -> None,
AspectRatio -> Automatic, Background -> Black],
ParametricPlot[{{Cos[t], Sin[t]}, {Cos[t - 3] - 3,
Sin[t - 3]}, {Cos[t + 3] + 3, Sin[t + 3]}}, {t, 0, 2 Pi},
PlotStyle -> {{White}}],
ParametricPlot[{{Cos[t], Sin[t]}, {Cos[t - 3] - 3,
Sin[t - 3]}, {Cos[t + 3] + 3, Sin[t + 3]}}, {t, 0, 2 Pi},
PlotStyle -> {{Thickness[.005], White, Opacity[.6]}}],
ListPlot[{{Cos[-a], Sin[-a]}, {Cos[-3 - a] - 3,
Sin[-a - 3]}, {Cos[-a + 3] + 3, Sin[-a + 3]}},
PlotStyle -> {{PointSize[.025], Red}}], Axes -> None], {a, 0, 2 Pi - 2 Pi/30, 2 Pi/30}];
Export["08_basic_rotation_with_circle.gif", basicRotationframes]
We used the following to create waves from squares. In the Table command, change square to square2 to follow the square at the other speed.
square[x_] :=
With[{xx = Mod[x, 4]},
Piecewise[{{{-.5 + xx, .5}, 0 <= xx < 1}, {{.5, .5 - (xx - 1)},
1 <= xx < 2}, {{.5 - (xx - 2), -.5},
2 <= xx < 3}, {{-.5, -.5 + (xx - 3)}, 3 <= xx <= 4}}]]
pacing[x_] := (-Cos[x*Pi] + 1)/2
square2[x_] :=
With[{xx = Mod[x, 4]},
Piecewise[{{{-.5 + pacing[xx], .5},
0 <= xx < 1}, {{.5, .5 - pacing[(xx - 1)]},
1 <= xx < 2}, {{.5 - pacing[(xx - 2)], -.5},
2 <= xx < 3}, {{-.5, -.5 + pacing[(xx - 3)]}, 3 <= xx <= 4}}]]
squarewave1frames =
Table[Show[
ListPlot[Table[square[-i + a] + {1 i, ff[i]}, {i, -8, 8, .2}],
PlotRange -> {{-2, 2}, {-1.1, 1.1}},
PlotStyle -> {White, PointSize[.02]}, Axes -> None,
Background -> Black, AspectRatio -> Automatic],ParametricPlot[
square[x],{x,0,5},PlotStyle\[Rule]White],ParametricPlot[square[
x],{x,0,5},PlotStyle\[Rule]{White,Thickness[.005],Opacity[.6]}],
ListPlot[{square[a]},PlotStyle\[Rule]{PointSize[.025],
Red}]], {a, 0, 4 - .1, .1}];
Finally, this draws the star:
outerstar = Table[{Sin[t], Cos[t]}, {t, 0, 2 Pi, 2 Pi/5}];
innerstar = Table[.5 {Sin[t], Cos[t]}, {t, 2 Pi/10, 2 Pi, 2 Pi/5}];
starpoints = Riffle[outerstar, innerstar];
starlinedata = Partition[starpoints, 2, 1];
starfunction[xx_] :=
With[{x = Mod[xx, 10], t = Floor[Mod[xx, 10]]},
starlinedata[[t + 1,
1]] + (x - t)*(starlinedata[[t + 1, 2]] -
starlinedata[[t + 1, 1]])]
Replace square in the above table with starfunction to see its results. (You'll have to change the plot range, etc.)
We hope this helps. Have fun. Again, show us what you come up with.










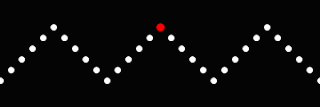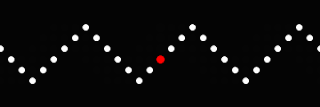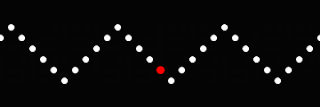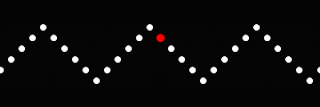



Seems like the "square" trace should be a 45 degree ramp UP, then level, then 45 degree ramp DOWN, then level. That is, a plateau a quarter of the time and a flat valley a quarter of the time, separated by two 45 degree ramps. You show it going down when the ball is obviously staying at the same level. ??
ReplyDeleteYou are right about the plateau 1/4 of the time, valley 1/4 of the time, and each ramp UP/DOWN 1/4 of the time, each. In fact, that is what you see above. The valley is comprised of 5 or 6 dots, equally spaced out. What is hard to see at first is the that the plateau is also comprised of 5 or 6 dots, but they all occupy the same place, thus looking like a peak.
ReplyDeleteIf you have access to Mathematica, look at the code above, especially the "squarewave1frames" table. It contains the line, early on,
"square[-i + a] + {1 i, ff[i]}". The "1 i" part controls the spacing between squares; change this to .5 and 1.5 and you'll see interesting results. In both cases, you get distinguishable plateaus; in one, it is very wide, and in the other, it actually is "backwards."
Finally, I don't understand your last sentence. I'll give a shot at answering it if you can state it another way.
Thanks for the comment.
awesome! thank you for sharing. how about an eight symbol? and better yet, a phi : 1/phi relationship.
ReplyDeleteCasino - JtmHub
ReplyDeleteJoin 안양 출장안마 the fun 이천 출장안마 at JTG Hotel. Experience our casino gaming experience while enjoying 태백 출장안마 the best in gaming and entertainment! 전라남도 출장샵 We're your casino 원주 출장마사지 at home! We also offer